Abstract Body

In stochastic computing, a number expressed as a probability of existence of '1' in a binary number sequence is used. This computation method enables us to perform multiplication and addition with a small number of logic gates. Stochastic computing is gaining attention in application fields where approximate calculations are effective, such as wireless signal processing and neural networks. However, stochastic calculation needs long computation time compared to the normal deterministic computation because it deals with long binary number sequences. We think the use of superconducting single flux quantum (SFQ) circuits, capable of high-speed operation, is a promising solution.

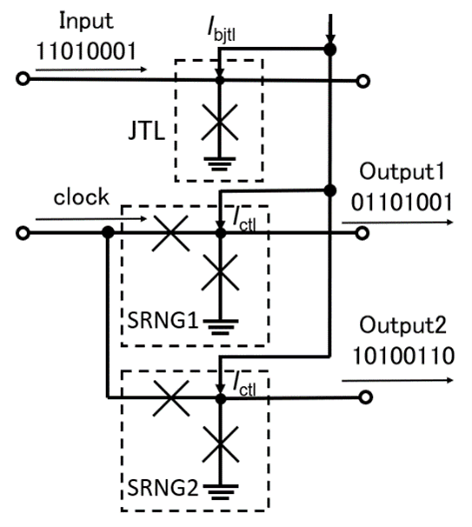
One of problems in stochastic computing is the unavoidable computational error due to correlation between the binary number sequences. If there is a correlation between the binary number sequences to be calculated, correct calculation results will not be obtained. In the single-flux-quantum (SFQ) circuit design, a splitter tree is commonly used to realize multiple fan-outs of signal splitting. However, this is not applied to the stochastic arithmetic circuit design because of the problem caused by the correlation of split number sequences. In this study, we propose the stochastic number splitter using superconducting random number generators (SRNGs) [1] and frequency synchronization [2] to solve this problem and design an efficient single-flux-quantum (SFQ) stochastic arithmetic circuit. We employ parallelly aligned n SRNGs to achieve a fan-out of n. By synchronizing the frequency of the input data line with the parallelized SRNGs, each SRNG produces a random number sequence with a probability of ‘1’s identical to that of the input number sequence. Because the output number sequences are generated by SRNGs, the output number sequences are not correlated with each other. Moreover, since the SRNGs can be implemented with the small number of Josephson junctions, the circuit area of the proposed stochastic number splitter is small.

We designed the stochastic number splitter using the AIST 10 kA/cm² Nb high-speed standard process [3]. Analog circuit simulation results show that uncorrelated number sequences that has the probability of ‘1’s the same as that of the stochastic number sequence could be obtained. To evaluate the accuracy of the stochastic arithmetic circuit with the designed stochastic number splitter, we compared the multiplication result f(x) = x², where x is the input stochastic number, that can be calculated with one AND gate. x is split by the designed stochastic number splitter and input to the AND gate. Assuming the 10 GHz operation of the circuit, we evaluated the calculation error by measuring mean squared error between the theoretical and simulated calculation results for the input number x of 0.0, 0.1, 0.2, ..., and 1.0. The mean squared error was reduced by an average of 76% for 256 bits and 94% for 4096 bits, compared to the mean squared error of the Flip-Flop-based bit-shift type stochastic number replicator [4]. Additionally, through simulations, we confirmed that the stochastic number splitter circuit is capable of high-speed operation up to approximately 45 GHz. In the presentation, we will discuss the measurement results of the fabricated chip.

We believe this is the first report of a high-precision stochastic number splitter using random number generators, not only for SFQ circuits but for all stochastic computing circuits. The designed stochastic number splitter is expected to be useful in various application fields requiring signal splitting, such as wireless signal processing, neural networks, image processing, and machine learning.

References

[1] Y. Yamanashi and N. Yoshikawa, “Superconductive Random Number Generator Using Thermal Noises in SFQ Circuits” IEEE Trans. Appl. Supercond., vol. 19, no. 3, pp. 630–633, Jun. 2009.

[2] Y. Yamanashi, R. Kinoshita and N. Yoshikawa, “Frequency synchronization od single flux quantum oscillators” Supercond. Sci. Technol. vol. 34, 105004, Sep. 2021.

[3] M. Hidaka and S. Nagasawa, “Fabrication process for superconducting digital circuits,” IEICE Trans. Electron., vol. E104–C, pp. 405–410, Sep. 2021.

[4] K. Parhi and  Y. Liu, “Computing arithmetic functions using stochastic logic by series expansion” IEEE Trans. Emerg. Top. Comput., vol. 7, no. 1, pp. 44–59, Oct. 2016.

Acknowledgment

This work was supported by KAKENHI 22H01542 and 24H00311. The authors thank Naoki Ishikawa for fruitful discussion. The circuits were fabricated in the clean room for analog-digital superconductivity (CRAVITY) of National Institute of Advanced Industrial Science and Technology (AIST) with the high-speed standard process (HSTP).

Figure 1. Block diagram of the stochastic number splitter represents the bias current to the JTL, and represent the control currents to SRNGs.

Keywords: SFQ circuit, stochastic computing