Abstract Body

We report the rotational instability of a superconducting magnetic bearing (SMB) system operating at about 10 K in a vacuum environment. An SMB has great potential in applications of low-energy loss systems. A typical SMB consists of a ring-shaped permanent magnet as a rotor that levitates over the high-temperature superconductor (HTS) array as a stator. We employ YBCO, a Type-II superconductor that pins the flux when it is cooled with the external magnetic field, so-called field-cooling. When the magnetic field of the rotor magnet has rotational symmetry about the axis of rotation, the HTS does not experience the change in the applied magnetic field. Thus, the rotor ring magnet rotates freely without any contact. This attractive feature enables us to construct a bearing with no mechanical contact, and thus no physical friction. As a result, the functionality of the SMB has low energy loss, and is capable of operating in low-temperature and vacuum environments, e.g., energy-storage flywheels [1-2], sensitive gravimeters [3], micro-force measurement [4], lunar telescopes [5], and polarimeters [6].

This attractive low-friction system can potentially add a challenge in the rotational kinetics. Any external torque in the rotational direction does not damp out immediately due to the low-loss system. As a result, the AC motor driven rotor can rotate with oscillation around the rotational frequency, and we investigated this effect.

We develop the rotational mechanism operating at the cryogenic temperature below 10 K. The rotational mechanism consists of the drive motor and the SMB. The rotor is held in place using three cryogenic holder mechanisms until the YBCO of SMB undergoes field cooling. The drive motor is based on a synchronous motor, the 72 alternative SmCo magnets, and the 18 sets of three-phase coils. The SMB consists of the 32 segmented SmCo magnets and the segmented bulk YBCO array. The inner diameter of the rotor magnet is 408 mm. The rotation rate of the rotor is reconstructed by an optical encoder, which consists of a disk with 128 slots on the rotor, the pair of LED and photodiode on the stator.

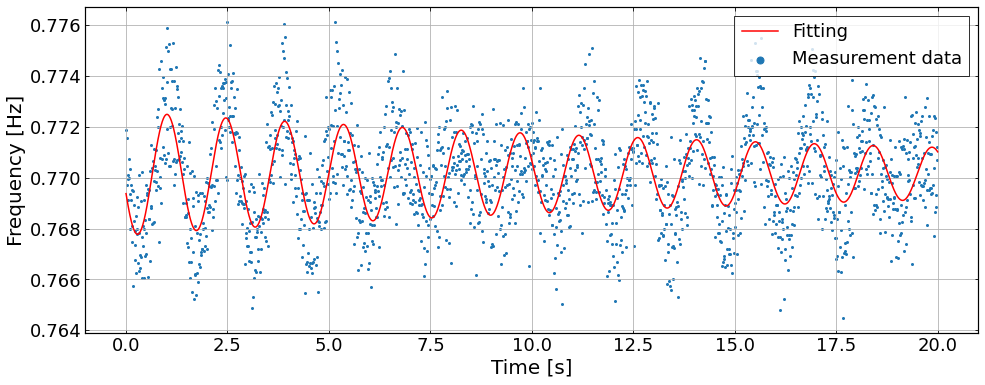
The test is conducted by placing the entire rotational mechanism in the cryostat cooled by a GM cooler, and the entire system is kept below the temperature of 10 K. The rotor is driven by the AC commanded by the motor driver placed outside the cryostat. The open-loop control drives this AC motor without any feedback for simplicity. One potential drawback is identified as the oscillation in rotation frequency around the target rotation frequency. Specifically, the rotor is accelerated from a stationary state to 0.8 Hz in the cryostat. The frequency is kept constant for several minutes, and then the rotation slows down and stops by disconnecting the motor driver cables. We reconstructed the rotation frequency by using the optical encoder signal. From the frequency data, we found that rotation frequency oscillates over time around the target frequency, and those oscillations were damped over time. The frequency amplitude of the oscillation is about 0.01 to 0.02 Hz, and the damping time constant is about 10 to 50 s. We also found that the frequency of the oscillation is roughly proportional to the square root of the drive current flowing through the coils.

We modeled this rotational instability with the oscillating and damping terms in the rotational direction. The potential physical correspondence of these terms is the magnetic potential between the rotor and the stator of the synchronous motor, and the eddy current in the motor and SMB. We investigate the obtained effective spring constant and the damping time constant with respect to the independently obtained estimates.

In this presentation, we report our rotational mechanism containing the synchronous motor and SMB, the experimental setup, and the experimental results of the axial rotational instability. We finally discuss the physical interpretation of the source of the rotational instability.

References

[1] Bornemann, H. J., T. Ritter, C. Urban, O. Paitsev, K. Peber, and H. Rietschel. 1994. “Low Friction in a Flywheel System Pith Passive Superconducting Magnetic Bearings.” Applied Superconductivity 2 (7-8): 439–47. 

[2] Hull, John R., Thomas M. Mulcahp, Kenneth L. Uherka, Robert A. Erck, and Robert G. Abboud. 1994. “Flywheel Energy Storage Using Superconducting Magnetic Bearings.” Applied Superconductivity 2 (7-8): 449–55.

[3] Hull, J. R., and T. M. Mulcahy. 1999. “Gravimeter Using High-Temperature Superconducting Bearing.” IEEE Transactions on Applied Superconductivity: A Publication of the IEEE Superconductivity Committee 9 (2): 390–93.

[4] Lee, Eunjeong, Ki Bui Ma, T. L. Wilson, and Wei-Kan Chu. 1999. “Characterization of Superconducting Bearings for Lunar Telescopes.” IEEE Transactions on Applied Superconductivity: A Publication of the IEEE Superconductivity Committee 9 (2): 911–15.

[5] Yang, Wenjiang, Yu Ji, Mao Ye, and Haibin Tang. 2019. “A Micro-Force Measurement System Based on High-Temperature Superconducting Magnetic Levitation.” Measurement Science & Technology 30 (12): 125020.

[6] Kusaka, A., T. Essinger-Hileman, J. W. Appel, P. Gallardo, K. D. Irwin, N. Jarosik, M. R. Nolta, et al. 2014. “Modulation of Cosmic Microwave Background Polarization with a Warm Rapidly Rotating Half-Wave Plate on the Atacama B-Mode Search Instrument.” The Review of Scientific Instruments 85 (2): 024501.

Figure 1. One example of the oscillation and damping of rotation frequency.

Keywords: Rotational instability, Superconducting magnetic bearing, Synchronous motor, Oscillation, Damping